KNN

KNN이란?

K-최근접 이웃 (K-NearestNeighbors)
Classification(분류)과 Regression(회귀)를 모두 지원한다
- Classification은 가장 가까운 K 원소 종류의 개수로 계산
- Regression은 가장 가까운 K 원소 값의 평균으로 계산
예측하려는 데이터와 주위에 있는 데이터의 거리를 측정해 가장 가까운 K개의 데이터를 참조해 분류 예측한다.
학습시 단순히 데이터를 저장하고 예측 시점에 거리를 계산한다.
- 학습은 빠르지만 예측시 시간이 많이 걸린다.
  K (Hyper Parameter)
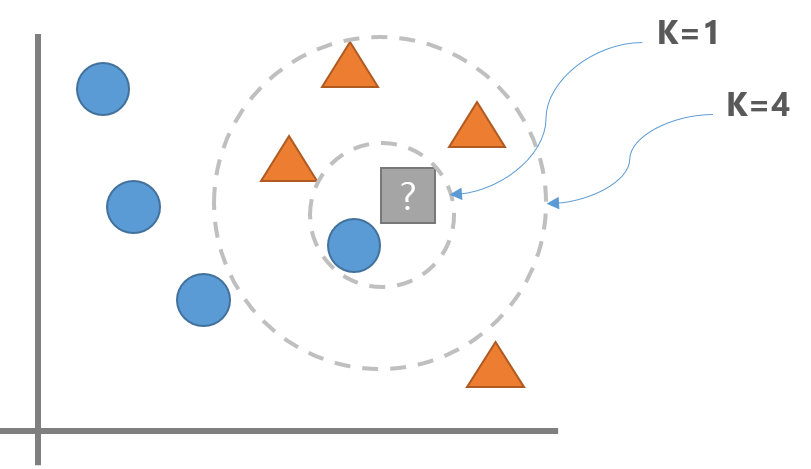
K는 새로운 데이터포인트를 분류할때 확인할 데이터 포인트의 개수를 지정하는 hyper parameter이다.

분류**
- K를 1로 하면 파란색, K를 3으로 하면 주황색 으로 분류한다.
**회귀**
- K를 1로 하면 파란색, K를 3으로 하면 주황색 data point의 평균값으로 추론한다.
K가 너무 작으면 Overfitting이 일어날 수 있고 K가 너무 크면 Underfitting이 발생할 수 있다.
- Overfitting: K값을 더 크게 잡는다.
- Underfitting: K값을 더 작게 잡는다

주요 Hyper Parameter

분류: sklearn.neighbors.KNeighborsClassifier, 회귀: sklearn.neighbors.KNeighborsRegressor
이웃 수
- n_neighbors = K
- n_neighbors는 Feature수의 제곱근 정도를 지정할 때 성능이 좋은 것으로 알려져 있다.
거리 재는 방법
- p=2: 유클리디안 거리(Euclidean distance - 기본값 - L2 Norm)
  - 제곱을 통해 거리계산 → 대각선
- p=1: 맨하탄 거리(Manhattan distance - L1 Norm)
  - 일반 거리로 거리계산 → 네모

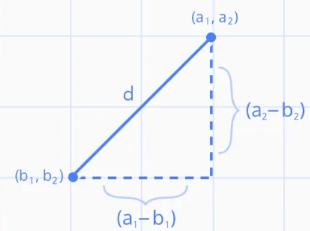
유클리디안 거리(Euclidean_distance)

\[distance = \sqrt{(a_1 - b_1)^2 + (a_2-b_2)^2}\\ n차원 벡터간의 거리 = \sqrt{(a_1 - b_1)^2 + (a_2-b_2)^2 +...+(a_n-b_n)^2}\]

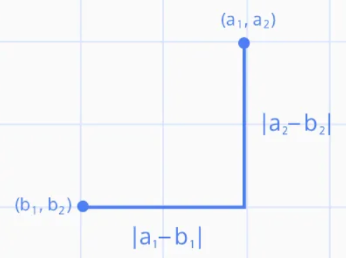
맨하탄 거리 (Manhattan distance)

\[distance = |a_1 - b_1| + |a_2 - b_2| \\ 𝑛차원벡터간의거리= |a_1 - b_1| + |a_2 - b_2| + ... + |a_n - b_n|\]

요약

장점

이해하기 쉬운 모델이며 튜닝할 하이퍼파라미터의 수가 적어 빠르게 만들 수있다.

단점

훈련세트가 너무 큰 경우(Feature나 관측치의 개수가 많은 경우) 거리를 계산하는 양이 늘어나 예측이 느려진다.
- 추론에 시간이 많이 걸린다.
Feature간의 값의 단위가 다르면 작은 단위의 Feature에 영향을 많이 받게 되므로 전처리로 Feature Scaling작업이 필요하다.
Feature가 너무 많은 경우와 대부분의 값이 0으로 구성된(희소-sparse) 데이터셋에서 성능이 아주 나쁘다

사용처

K-NN은 서비스할 모델을 구현할때 보다는 복잡한 알고리즘을 적용해 보기 전에 확인용 또는 base line을 잡기 위한 모델로 사용한다.
- 주로 K-NN 결과 보다 더 좋은 모델을 만들어야 한다.(기준)

SVM

SVM이란?

Support Vector Machine
딥러닝 이전에 분류에서 뛰어난 성능으로 많이 사용되었던 분류 모델
하나의 분류 그룹을 다른 그룹과 분리하는 최적의 경계를 찾아내는 알고리즘
중간 크기의 데이터셋과 특성이(Feature) 많은 복잡한 데이터셋에서 성능이 좋은 것으로 알려져있다.

Linear(선형) SVM

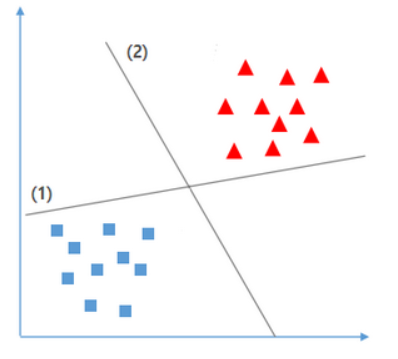
Linear SVM 예시

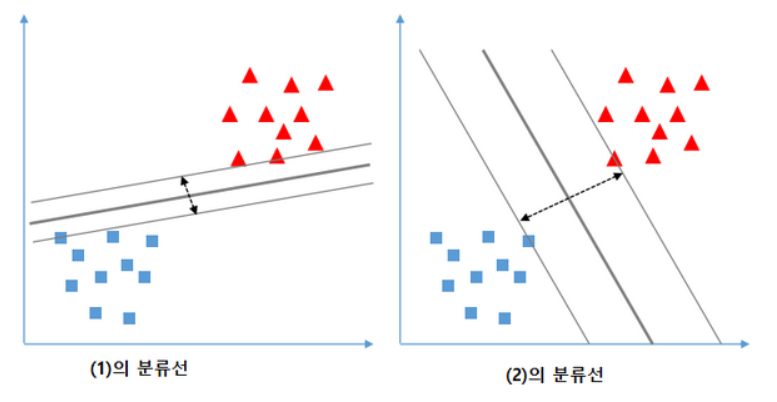
train 데이터의 경우에는 (1)의 경우가 최적의 분류이지만 지도학습을 하는 이유는 새로운 데이터를 바탕으로 결과값을 도출 해야 하기 때문에 (2)의 경우가 최적의 분류를 위한 경계선이 된다.
- 데이터 간의 거리가 가까울 수록 분류선과 가까운 데이터 값이 틀릴 가능 성이 높아진다.
Linear SVM 모델은 두 클래스 간의 거리를 가장 넓게 분리할 수있는 경계선을 찾는 것을 목표로 한다.

SVM의 목표

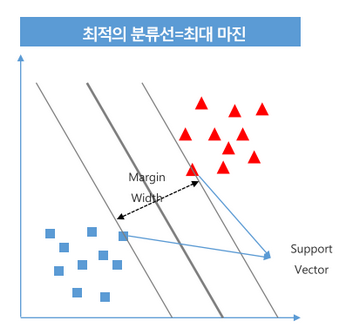
support vector간의 가장 넓은 margin을 가지는 decision boundary(결정 경계)를 찾는다.
- Support Vector: 경계를 찾는데 기준이 되는 데이터포인트. 결정경계에 가장 가까이 있는 vector(데이터포인트)를 말한다.
- margin: 두 support vector간의 너비
margin이 넓은 결정경계를 만드는 함수를 찾는 것.

규제 - Hard Margin, Soft Margin

TrainSet에 Outlier(이상치)들이 있다면 데이터를 완벽하게 나눌 수는 없다 -> Overfitting
Margin을 나눌 때 Outlier를 얼마나 무시할 것인지에 따라 Hard margin과 soft margin으로 나뉜다.
Outlier들을 무시하게 된다면 좀 더 넓은 margin을 얻을 수 있다.

Hard margin

Outlier들을 무시하지 않고 Support Vector를 찾는다.
Margine이 Soft Margin에 비해 매우 좁다.
Overfitting이 발생할 수 있다.

Soft margin

일부 Outlier들을 무시하고 Support Vector를 찾는다.
Margin의 거리가 넓다.
Underfitting이 발생할 수 있다.

Hyper Parameter C

Outlier 을 무시하는 비율을 설정하는 Hyper Parameter
기본값 1
Parameter 값을 크게 주면 제약조건이 강해진다.
- Margin 값이 작아진다.
- 오류가 작아진다.
- Overfitting이 일어날 가능성이 크다.
Parameter 값을 작게 주면 제약조건이 약해진다.
- Margin 값이 커진다.
- Test data에서 성능이 안좋아지나 generalization(일반화)되어 테스트 데이터 성능이 올라간다.
- Overfitting이 일어날 가능성이 크다.
  Linear SVM에서 C의 변화에 따른 성능변화 확인
overfitting: C의 값을 줄인다.
underfitting: C의 값을 늘린다.

Kernel SVM

None Linear(비선형) SVM
차원을 변경 해서 비선형 데이터셋을 선형으로 분리한다.

Kernel trick(커널 트릭)

비선형 데이터셋을 선형으로 분리하기 위해 차원을 변경해야 하는데 이때 사용하는 함수를 Kernel이라고 하고 차원을 변경하는 것을 kernel trick 이라고 한다.
대표적인 kernel함수
- Radial kernel - Default
- Polynomial kernel
- Sigmoid kernel

Non linear SVM 모델의 Hyper Parameter

C

오차 허용기준관련 규제.
- 기본 값은 1이며 클수록 규제를 강하게 하고 작을 수록 규제를 약하게 한다.
  gamma
Kernel함수 규제 값.
- 기본 값은 1이며 클수록 규제를 강하게 하고 작을 수록 규제를 약하게 한다.

c와 gamma

C, gamma: 큰값: 복잡한 모델(강한 규제), 작은값 - 단순한 모델. (약한 규제)
- overfitting: C, gamma 값들을 감소
- undefitting: C, gamma 값들을 증가

SVC에서 predict_proba() 때 주의할 점

ROC AUC score, AP score
- 모델이 예측한 양성의 확률 ==> model.predict_proba(X)
SVC에서 predict_proba()는 호출이 기본적으로는 막혀있다.
따라서 roc-auc score나 average precision score를 계산하기 위해서는 SVC(probability=True)해야 predict_proba()를 사용할 수 있다.

[Machine Learning] 07. 지도학습

KNN