선형회귀 개요
선형 회귀(線型回歸, Linear regression)는 종속 변수 y와 한 개 이상의 독립 변수X와의 선형 상관 관계를 모델링하는 회귀분석 기법. 위키백과
선형회귀 모델
- 각 Feature들에 가중치(Weight)를 곱하고 편향(bias)를 더해 예측 결과를 출력한다.
- Weight와 bias가 학습 대상 Parameter가 된다.
- $\hat{y_i}$: 예측값
- $x$: 특성(feature-컬럼)
- $w$: 가중치(weight), 회귀계수(regression coefficient). 특성이 $\hat{y_i}$ 에 얼마나 영향을 주는지 정도
- $b$: 절편
- $p$: p 번째 특성(feature)/p번째 가중치
- $i$: i번째 관측치(sample)
LinearRegression
- 가장 기본적인 선형 회귀 모델
- 각 Feauture에 가중합으로 Y값을 추론한다.
데이터 전처리
선형회귀 모델사용시 전처리
- 범주형 Feature
- : 원핫 인코딩
- 연속형 Feature
- Feature Scaling을 통해서 각 컬럼들의 값의 단위를 맞춰준다.
- StandardScaler를 사용할 때 성능이 더 잘나오는 경향이 있다.
- 범주형 Feature
다항회귀 (Polynomial Regression)
- 전처리방식 중 하나로 Feature가 너무 적어 y의 값들을 다 설명하지 못하여 underfitting이 된 경우 Feature를 늘려준다.
- 각 Feature들을 거듭제곱한 것과 Feature들 끼리 곱한 새로운 특성들을 추가한다.
- 파라미터 가중치를 기준으로는 일차식이 되어 선형모델이다. 파라미터(Coef, weight)들을 기준으로는 N차식이 되어 비선형 데이터를 추론할 수 있는 모델이 된다.
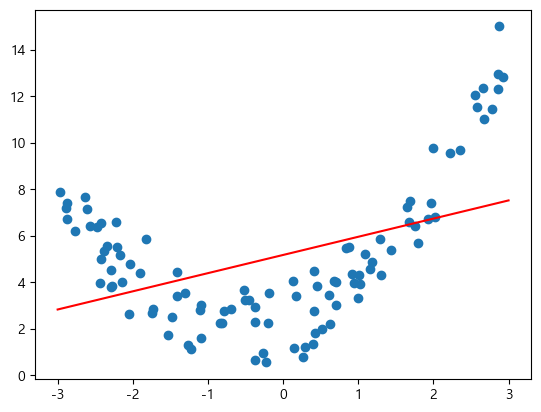
PolynomialFeaturesTransformer를 사용해서 변환한다.- 단항 회귀 결과 → Underfitting
단항 회귀의 결과 값을 보면 특정 부분에서는 잘 예측하지만 다른 곳은 예측을 잘 하지 못하는 것을 볼 수 있다.
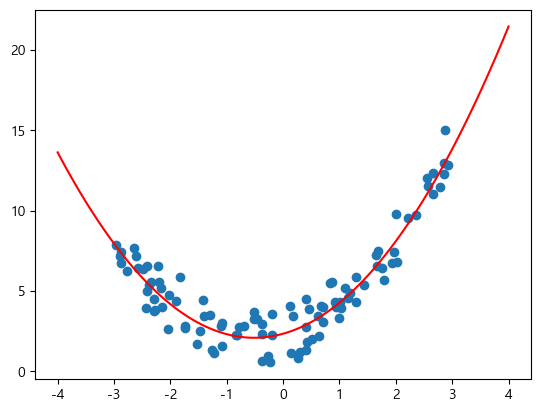
다항 회귀 결과
degree=2
- 두 결과 값의 차이
- 대신 다항회귀에서 Feature 수가 너무 많으면, 즉 degree를 너무 크게 하면 Overfitting 문제가 생긴다
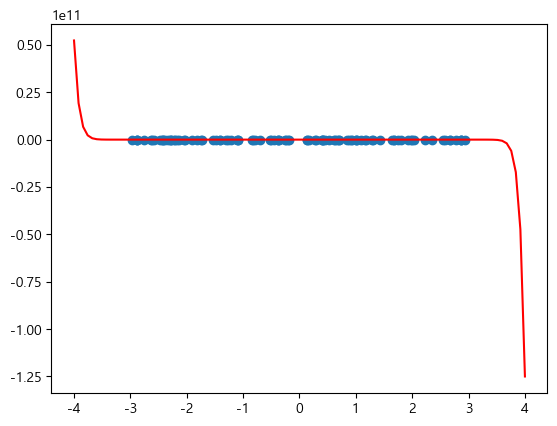
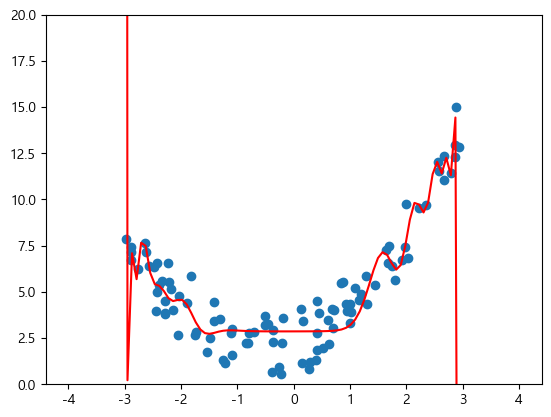
degree=35로 정의 했을 때 결과 → Overfitting
- 좀더 가까이서 봤을 때
→ 위와 같은 문제(overfitting)이 발생하기 때문에 Regularization이 필요하다.
- feature가 적다 -> underfitting -> 늘린다, regularization
- feature가 너무 많다 -> overfitting -> 줄인다, regularization
규제 (Regularization)
- 선형 회귀 모델에서 과대적합(Overfitting) 문제를 해결하기 위해 가중치(회귀계수)에 페널티 값을 적용한다.
- 입력데이터의 Feature들이 너무 많은 경우 Overfitting이 발생.
- Feature수에 비해 관측치 수가 적은 경우 모델이 복잡해 지면서 Overfitting이 발생한다.
- 해결
- 데이터를 더 수집한다.
- Feature selection
- 불필요한 Features들을 제거한다.
- 규제 (Regularization) 을 통해 Feature들에 곱해지는 가중치가 커지지 않도록 제한한다.(0에 가까운 값으로 만들어 준다.)
- LinearRegression의 규제는 학습시 계산하는 오차를 키워서 모델이 오차를 줄이기 위해 가중치를 0에 가까운 값으로 만들도록 하는 방식을 사용한다.
- L1 규제 (Lasso) -> 그냥 더한다
- L2 규제 (Ridge) -> 제곱해서 더한다.
Ridge Regression (L2 규제)
- 손실함수(loss function)에 규제항으로 $\alpha \sum_{i=1}^{n}{w_{i}^{2}}$ (L2 Norm)을 더해준다.
- $\alpha$는 하이퍼파라미터로 모델을 얼마나 많이 규제할지 조절한다.
- $\alpha = 0$ 에 가까울수록 규제가 약해진다. (0일 경우 선형 회귀동일)
- $\alpha$ 가 커질 수록 모든 가중치가 작아져 입력데이터의 Feature들 중 중요하지 않은 Feature의 예측에 대한 영향력이 작아지게 된다.
손실함수(Loss Function): 모델의 예측한 값과 실제값 사이의 차이를 정의하는 함수로 모델이 학습할 때 사용된다.
ElasticNet(엘라스틱넷)
- 릿지와 라쏘를 절충한 모델.
- 규제항에 릿지, 라쏘 규제항을 더해서 추가한다.
- 혼합비율 $r$을 사용해 혼합정도를 조절 $r$ -> rate
- $r=0$이면 릿지와 같고 $r=1$이면 라쏘와 같다.
정리
- 일반적으로 선형회귀의 경우 어느정도 규제가 있는 경우가 성능이 좋다.
- 기본적으로 Ridge를 사용한다.
- Target에 영향을 주는 Feature가 몇 개뿐일 경우 특성의 가중치를 0으로 만들어 주는 Lasso 사용한다.
- 특성 수가 학습 샘플 수 보다 많거나 feature간에 연관성이 높을 때는 ElasticNet을 사용한다.
정리
- 일반적으로 선형회귀의 경우 어느정도 규제가 있는 경우가 성능이 좋다.
- 기본적으로 Ridge를 사용한다.
- Target에 영향을 주는 Feature가 몇 개뿐일 경우 특성의 가중치를 0으로 만들어 주는 Lasso 사용한다.
- 특성 수가 학습 샘플 수 보다 많거나 feature간에 연관성이 높을 때는 ElasticNet을 사용한다.