로지스틱 회귀 (LogisticRegression)
- 선형회귀 알고리즘을 이용한 이진 분류 모델
- Sample이 특정 클래스에 속할 확률을 추정한다.
확률 추정
- 선형회귀 처럼 입력 특성(Feature)에 가중치 합을 계산한 값을 로지스틱 함수를 적용해 확률을 계산한다.
\[\hat{p} = \sigma \left( \mathbf{w}^{T} \cdot \mathbf{X} + \mathbf{b} \right)\\ \hat{p}:\: positive의\,확률,\quad \sigma():\:logistic\,함수,\quad \mathbf{w}:\:weight,\quad \mathbf{X}:\:input feature,\quad \mathbf{b}:\:bias\]
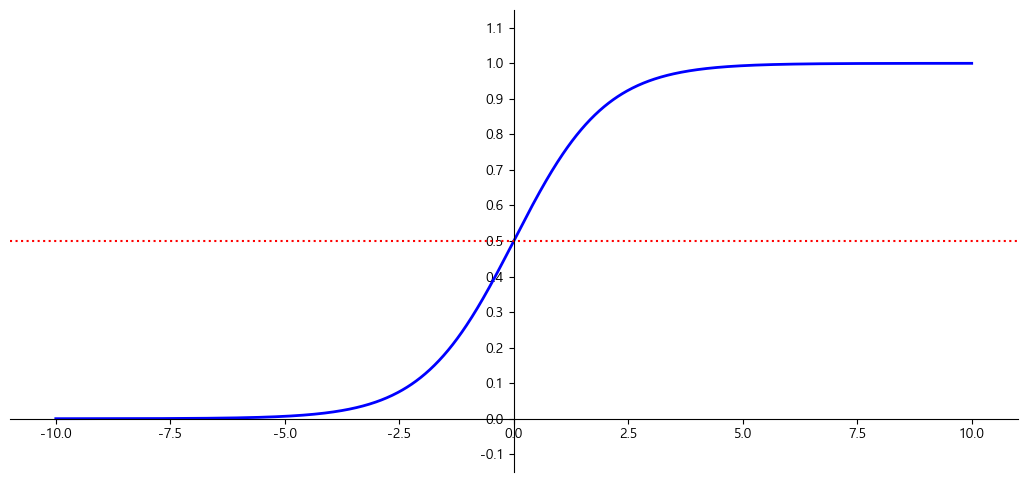
로지스틱 함수
- 0과 1사이의 실수를 반환한다.
- S 자 형태의 결과를 내는 시그모이드 함수(sigmoid function) 이다.
\[\sigma(x) = \frac{1}{1 + \mathbf{e}^{-x}}\]
\[\hat{y} = \begin{cases} 0\quad\hat{p}<0.5\\1\quad\hat{p}\geqq0.5 \end{cases}\]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| import matplotlib.pyplot as plt
import numpy as np
def logistic_func(X):
return 1 / (1 + np.exp(-X))
X = np.linspace(-10, 10, 1000)
y = logistic_func(X)
plt.figure(figsize=(13, 6))
plt.plot(X, y, color='b', linewidth=2)
plt.axhline(y=0.5, color='r', linestyle=':')
plt.ylim(-0.15, 1.15)
plt.yticks(np.arange(-0.1,1.2,0.1))
ax = plt.gca()
ax.spines['left'].set_position("center")
ax.spines['bottom'].set_position(('data', 0))
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.show()
|
LogisticRegression의 손실 함수(Loss Function)
- Cross Entropy(로그손실-log loss)
- 모델이 예측한 정답의 확률에 대해 log를 취해 손실값을 구한다.
- 확률이 틀리면 틀릴 수록 손실값을 크게 만들기 위해서 log를 취한다.
\[\log{\left(모델이\,예측한\,정답에\,대한\,확률\right)}\]
- Binary Cross Entropy
- Logistic 함수를 이용한 추론 결과에 대한 cross entropy 계산
- Logistic함수은 positive(1)의 확률만 추출하므로 정답이 0일때, 1일때 계산하는 것이 다르다. 그것을 하나의 공식으로 정의한 것이 binary cross entropy이다. \(L(\mathbf{W}) = - \frac{1}{m} \sum_{i=1}^{m}{\left[ y_{i} \log{\left( \hat{p}_i \right)} + \left( 1 - y_i \right) \log{\left( 1 - \hat{p}_i \right)} \right]}\\ y:\:실제값(정답),\quad\hat{p}:\:예측확률(양성확률)\)
- y(실제값) 이 1인 경우 $y_{i}\log{\left(\hat{p}_i\right)}$ 이 손실을 계산
- y가 0인 경우 $\left( 1 - y_i \right) \log{\left( 1 - \hat{p}_i \right)}$이 손실을 계산
- $\hat{p}$(예측확률)이 클수록 반환값은 작아지고 작을 수록 값이 커진다.
- Loss Function
- 모델이 예측한 값과 정답간의 차이(오차, loss)를 구하는 함수.
- 모델의 파라미터를 최적화할 때 loss를 최소화하는 것을 목적으로 한다.
최적화
최적화란
- 모델이 예측한 결과와 정답간의 차이(오차)를 가장 적게 만드는 Parameter를 찾는 과정을 최적화라고 한다.
- 모델의 예측값과 실제 값의 차이를 계산하는 함수를 만들고 그 값이 최소가 되는 지점을 찾는 작업을 한다.
목적함수(Object Function), 손실함수(Loss Function), 비용함수(Cost Function), 오차함수(Error Function)
- 모델의 예측한 값과 실제값 사이의 차이를 정의하는 함수로 모델이 학습할 때 사용된다.
- 이 함수의 반환값(Loss)을 최소화 하는 파라미터을 찾는 것이 최적화의 목적
- 해결하려는 문제에 맞춰 Loss 함수를 정의한다.
- Classification(분류)의 경우 cross entropy(log loss)를 사용한다.
- Regression(회귀)의 경우 MSE(Mean Squared Error)를 사용한다.
LogisticRegression의 최적화
- 분류 문제이므로 Cross entropy(Log loss함수)를 손실함수로 사용한다.
- Cross entropy는 loss의 최소값으로 하는 parameter 찾는 방정식이 없기 때문에 LogisticRegression은 경사하강법을 이용해 최적화를 진행한다.
- 로그 손실을 $\mathbf{W}$로 미분하면 다음과 같다.
- 아래 도함수로 기울기를 구해 기울기가 0이 될 때 까지 W(가중치)들을 update한다. \(\frac{\partial}{\partial w_j}L(W) = \frac{1}{m} \sum_{i=1}^{m}{\left( \sigma \left( \mathbf{W}^{T} \cdot \mathbf{x}_i \right) - \mathbf{y}_i \right)} x_{ij}\)
LogisticRegression 주요 하이퍼파라미터
- penalty: 과적합을 줄이기 위한 규제방식
- ‘l1’, ‘l2’(기본값), ‘elasticnet’, ‘none’
- C: 규제강도(기본값 1) - 작을 수록 규제가 강하다(단순).
- max_iter(기본값 100) : 경사하강법 반복횟수